18. Sequences

a2. Plots

To visualize a sequence we can make a table and plot it. The terms are plotted as a function of the index.

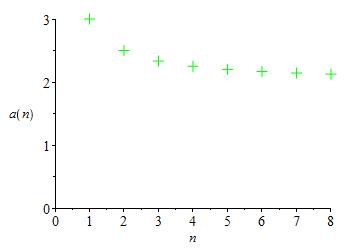
Make a table and plot of the sequence \(a_n=\dfrac{2n+1}{n}\) for \(n=1,2,3,\ldots\).

Here are the table and the plot:

\(n\)	\(1\)	\(2\)	\(3\)	\(4\)	\(5\)	\(6\)	\(7\)	\(8\)
\(a_n\)	\(3\)	\(\dfrac{5}{2}\)	\(\dfrac{7}{3}\)	\(\dfrac{9}{4}\)	\(\dfrac{11}{5}\)	\(\dfrac{13}{6}\)	\(\dfrac{15}{7}\)	\(\dfrac{17}{8}\)

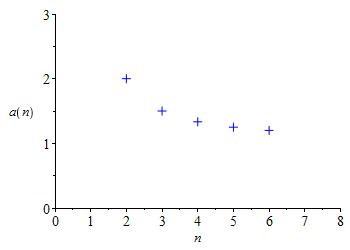
Plot the first \(5\) terms of the sequence \(a_n=\dfrac{n}{n-1}\) for \( n=2,3,4,\cdots\)

\(n\)	\(2\)	\(3\)	\(4\)	\(5\)	\(6\)
\(a_n\)	\(\dfrac{2}{1}\)	\(\dfrac{3}{2}\)	\(\dfrac{4}{3}\)	\(\dfrac{5}{4}\)	\(\dfrac{6}{5}\)